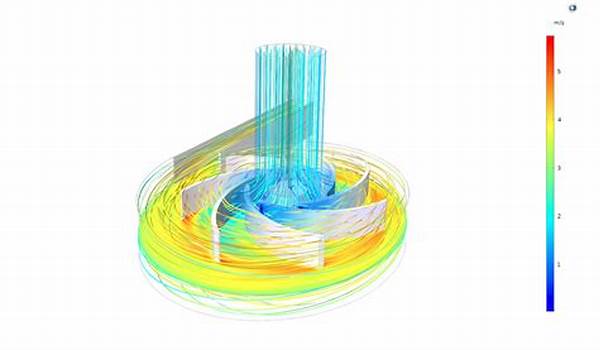
Hey there, fellow tech enthusiasts and curious minds! Today, we’re diving into the world of computational fluid dynamics (CFD) and exploring the fascinating ways multigrid methods are shaking things up. If you’re not familiar with CFD, it’s all about using computers to simulate how fluids—think air, water, and even more exotic substances—flow in various environments. It’s a big deal in industries ranging from aerospace to shipbuilding, helping engineers predict and optimize fluid behavior. But here’s the catch: these simulations can be computationally expensive and time-consuming. That’s where multigrid methods in CFD solvers come to the rescue.
Read Now : Advanced Nonlinear Dynamic Responses
Understanding the Basics of Multigrid Methods
Alright, so let’s break it down. Multigrid methods in CFD solvers are all about speeding up the process of solving equations that describe fluid flow. Imagine trying to solve a huge puzzle; traditionally, it would take forever to tackle it piece by piece. But with multigrid approaches, you can work on different parts of the puzzle simultaneously at various scales. These methods cleverly use a hierarchy of grid resolutions to accelerate convergence. By cycling through finer and coarser grids, solvers can smooth out errors more quickly. This nifty trick helps CFD practitioners save heaps of computational resources and time, making it possible to tackle intricate fluid dynamics problems without waiting a lifetime for results.
Multigrid methods in CFD solvers shine particularly when dealing with complex simulations. For example, in aerospace applications, accurately predicting airflow over an aircraft’s surface can lead to improved designs and fuel efficiency. Similarly, in automotive engineering, efficient CFD simulations help create cars that glide through the air like butter. By reaping the benefits of multigrid methods, engineers can access faster solutions, tweak designs with ease, and ultimately push technological boundaries. So next time you see a sleek airplane or a zippy sports car, remember the power of multigrid methods that helped shape them.
Practical Applications of Multigrid Methods
1. Speeding Up Simulations: Multigrid methods in CFD solvers slash computation times, enabling faster design iterations and quicker decision-making, vital in dynamic industries.
2. Aerospace Advancements: Aerospace engineers rely on these methods to predict airflow and optimize wing designs, leading to more energy-efficient and sustainable flights.
3. Automotive Innovations: Car designers use multigrid methods to refine vehicle aerodynamics, boosting fuel economy and reducing emissions—a win for both the environment and drivers.
4. Improved Energy Sector Solutions: Multigrid methods assist in simulating fluid dynamics within pipelines or reactors, enhancing energy efficiency and optimizing performance.
5. Environmental Impact Assessments: These methods empower simulations that help assess flow-related environmental impacts, aiding in sustainable decision-making.
How Multigrid Methods Enhance Efficiency
Let’s talk efficiency, folks. You know how frustrating it is when your computer takes forever to load a webpage or a video? Now imagine dealing with colossal amounts of data and calculations involved in CFD. Without multigrid methods in CFD solvers, engineers would be stuck waiting ages for results. The beauty of these methods lies in their ability to smooth out errors at different scales, meaning simulations converge faster than ever.
Think of it like giving each problem solver a specific job part in a larger assembly line. Instead of relying on one worker to do the entire assembly, you have a team working simultaneously at various stages, dramatically speeding up the process. This division of labor results in more efficient and accurate simulations, empowering engineers to make informed decisions in real-time—be it tweaking an aircraft design or reimagining a wind turbine. Thanks to multigrid methods, we streamline CFD, saving both time and precious resources.
Real-World Impact of Multigrid Methods
1. Empowering Engineers: Multigrid methods in CFD solvers empower engineers with quicker results, freeing their creativity to innovate and solve complex real-world challenges.
2. Fuel Efficiency Gains: In aviation, the contribution of multigrid methods results in more fuel-efficient aircraft designs, cutting down on operating costs and environmental impact.
3. Enabling Sustainability: By making CFD more accessible, multigrid methods support efforts towards sustainable development, from smarter buildings to eco-friendly vehicles.
4. Meeting Industry Demands: With multigrid methods, the industry can keep pace with fast-paced development cycles and evolving market demands, ensuring competitiveness.
5. Enhancing Research Capacity: These methods unlock potential in research, paving the way for scientific breakthroughs in fluid dynamics and applied engineering.
Read Now : Simulation Of Natural Physical Interactions
6. Optimizing Infrastructure: Multigrid methods aid in the efficient design of infrastructure projects like bridges and tunnels, ensuring safety and resource optimization.
7. Meeting Future Challenges: As global challenges evolve, multigrid methods equip scientists and engineers with the tools needed to address new and unforeseen fluid dynamics problems.
8. Reducing Carbon Footprint: By optimizing fluid flow simulations, industries can design systems with a lower carbon footprint, contributing to global sustainability goals.
9. Supporting Education: As multigrid methods enhance CFD simulations, more students gain hands-on experience, fostering the next generation of skilled engineers.
10. Championing Innovation: The rapid problem-solving capabilities of multigrid methods nurture innovation, pushing the boundaries in diverse fields from medicine to renewable energy.
The Technical Side of Multigrid Methods
Ready to geek out a little? The beauty of multigrid methods in CFD solvers lies in their technical prowess. At the core, these methods tackle the inherent challenges of solving partial differential equations, which form the backbone of fluid dynamics simulations. By employing a systematic approach, they break down complicated problems into manageable bits and pieces, allowing solvers to tackle them with finesse.
In simpler terms, imagine having a giant tangled ball of yarn. Multigrid methods help engineers untangle it strand by strand, then reweave it into a coherent solution. By leveraging the strengths of both fine and coarse grids, these solvers streamline the process and eliminate computational bottlenecks. The efficient use of resources allows engineers to focus on refining models, running simulations, and interpreting results. It’s like having a supercharged brain processing information at lightning speed.
Bridging Science and Industry
Infusing scientific techniques into industry practices can sometimes feel like trying to merge oil and water. But with multigrid methods in CFD solvers, the two blend seamlessly. By bridging the gap between theoretical development and practical applications, these methods empower industries with the best of both worlds.
In essence, multigrid methods simplify and expedite the process. Scientists and researchers gain the confidence to push the boundaries of their work, translating theories into tangible innovations. Meanwhile, industries benefit from faster solutions and optimally refined designs, meeting market demands head-on. This harmonious synergy fosters a culture of collaboration where science and industry walk hand in hand, propelling us all forward.
A Summary of Multigrid Magic
So there you have it, folks—the magic of multigrid methods in CFD solvers unraveled! As the world continues to evolve, these methods become indispensable tools for both researchers and industries alike. By streamlining simulations and expediting problem-solving, they shape safer, cleaner, and more efficient systems across the board.
In the grand scheme of things, these methods are endowing engineers with the ability to tackle fluid dynamics challenges with speed and precision. From shaping the aerodynamic contours of a car to assessing the impact of complex systems on the environment, multigrid methods equip us to handle the tasks of tomorrow. As we navigate the currents of innovation, let us celebrate this unsung hero of computational fluid dynamics. Here’s to multigrid methods—the engines driving progress in the world of CFD!